Electric Flux And Gauss's Law
What's In This Article...
Before we go ahead and tackle Electric Flux and Gauss’s Law, we should know all these prerequisites.
Continuous Charge Distribution
Linear Charge Density
- Charge q spread over length L Uniformly.
- Charge per unit length = q/l (linear charge density).
- Linear Charge Density, λ = q/l = dq/dl.
- Unit is Coulomb per meter, Cm-1.
- Hence, Charge in lenght L = Q = λL.
Surface Charge Density
- Charge q spread over an area 'a' uniformly.
- Charge per unit are = q/a.
- Surface Charge Density σ = q/a = dq/da.
- Unit is Coulomb per square meter, Cm-2.
- Hence, Charge in area 'A' = Q = σA.
Volume Charge Density
- Charge q spread over a volume 'v' uniformly.
- Charge per unit volume = q/v.
- Volume Charge Density ρ = q/v = dq/dv.
- Unit is Coulomb per cubic meter, Cm-3.
- Hence, Charge in volume V = ρV.
Area Vector
Though we know that the area of a surface is a scalar quantity, when its orientation affects the quantity, it may be treated as a vector quantity.
The area vector of a surface is a vector having magnitude equal to the area of surface and its direction is taken along the normal to the surface.
 = Aû
where û is the unit vector in the direction normal to the surface.
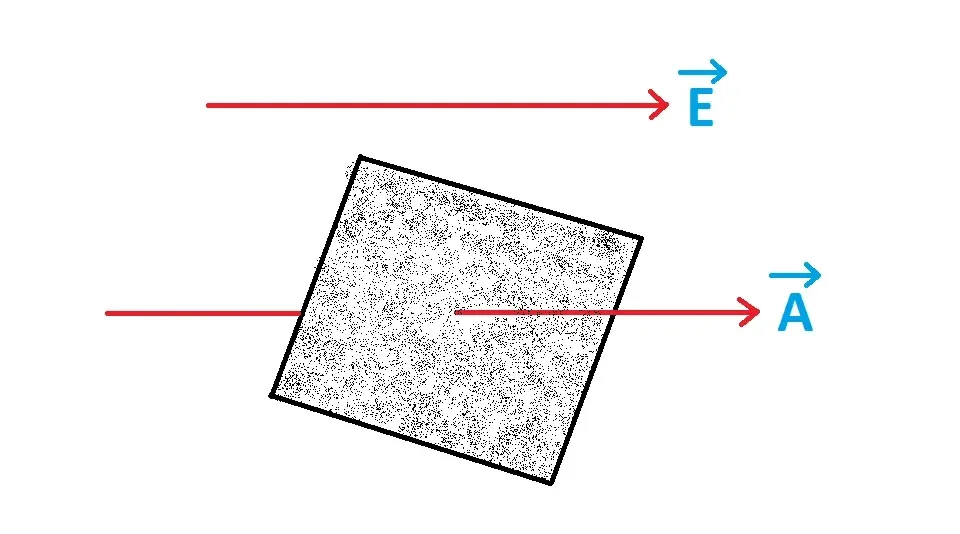
Each surface (not closed) has two directions of normal on it. So, for simplicity we take the direction of the area vector (Â) along the direction of the electric field.
And for a closed surface direction the area vector (Â) is always taken along normal and in the outside direction.
Electric Flux
When a surface is kept in an electric field, electric lines of force or electric field lines pass through it.
The number of electric field lines passing through a surface kept in an electric field, determines the electric flux associated/linked/passing through that surface.
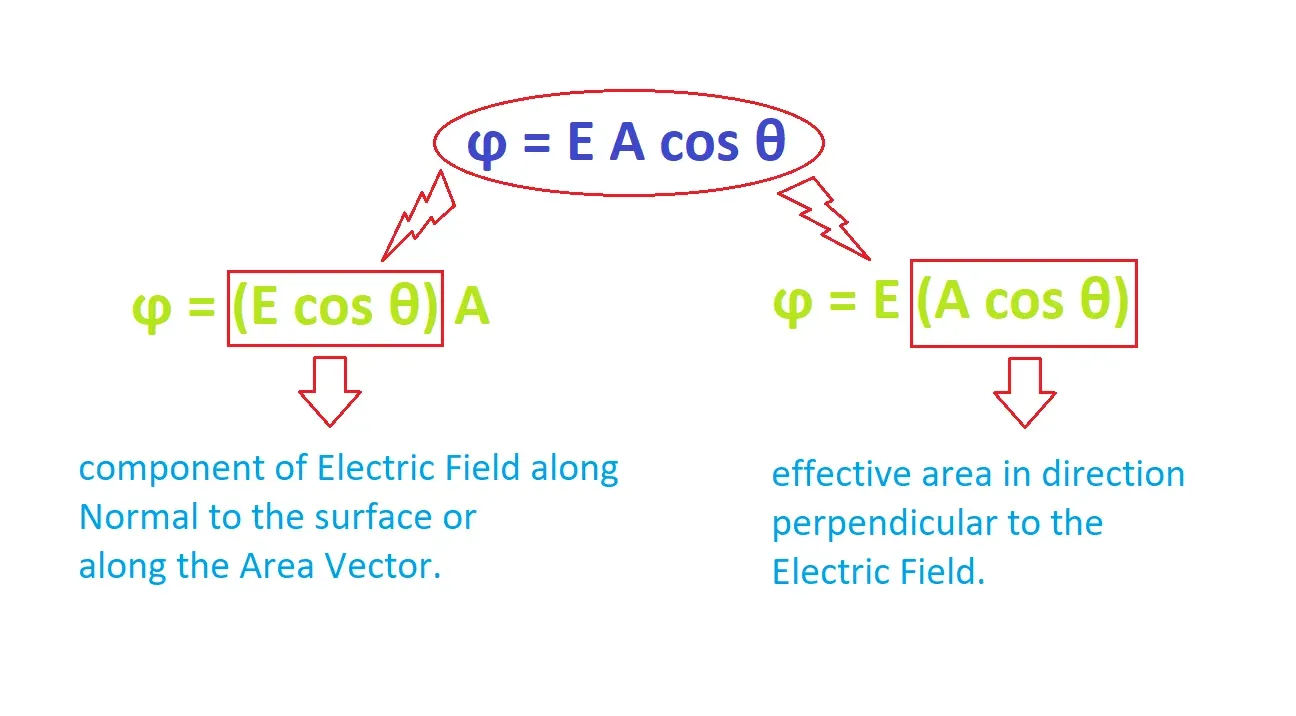
The Electric Flux passing through a surface in an electric field is determined as the scalar product of the intensity of electric field and the area vector of the surface. It is a Scalar Quantity.
φ = Ê.Â
φ = E A cosθ
θ = angle between Ê and Â.
Unit: Nm2C-1
Dimensional Formula: [ML3T-3A-1]
φ = ∫Ê.d (for non uniform electric field).
The above given formula for electric flux is more trusted by everyone and me too as this can be used in any conditions.
Gauss's Law
The total electric flux passing through a closed surface is 1/∊₀ times the net electric charge enclosed inside a surface.
φ = 1/∊₀ (net charge enclosed).
net charge enclosed = ΣQ
φ = ∫Ê.d = ΣQ/∊₀
Application of Gauss's Law
Gauss's Law is one of the fundamental laws of physics and it is used in a variety of areas or branches.
Here are given 3 theoretical applications of Gauss's Law:
Derivation of Coulomb's Law from Gauss's Law
Consider a spherical Gaussian surface and a charge 'q' is present inside the sphere at center. Radius of the sphere is 'R'.
Flux through a small area element d is:
dφ = Ê.d = E dA cos0° = E dA
Total electric flux through the whole sphere is:
φ = ∮dφ = ∮E dA = E ∮dA = E(4πR²) --eq(1)
due to symmetry ∮dA = 4πR²
∮: known as closed integral, used for closed surfaces.
According to Gauss's law, the same flux can also be written as:
φ = ΣQ/(∊₀K) --eq(2)
Now, equating equation 1 and 2, we get:
ΣQ/(∊₀K) = E(4πR²)
E = (1/4π∊₀K)(ΣQ/R²)
If a point charge 'q' is kept on the anywhere Gaussian surface then the Electrostatic force on 'q' due to ΣQ (=Q) will be
F = q E
Therefore, F = (1/4π∊₀K)(q Q/R²)
This is Coulomb's Law.
Electric Field near a Uniformly Charged Linear conductor of Infinite lenght
Its formula is given here:
E = λ/2π∊₀r
λ: Linear Charge Density.
Electric Field near a Uniformly Charged Sheet of Infinite Dimension
It's formula is given here:
Case I: When there is only a sheet of charges, here two opposite sides of a sheet are not separable.
E = σ/2∊₀
Case II: When the two sides are separable or the thickness is of some significance.
E = σ/∊₀










Comments
Post a Comment
thinking what to write...