What's In This Article...
Electric Dipole
Definition Of Electric Dipole
An electric dipole is a very stable system of two charge particles, equal in magnitude and opposite in nature, placed at a very small distance apart.
For ex: HCl molecule.
Electric Dipole Moment
Electric dipole moment of an electric dipole is defined as the product of the magnitude of one of the two charges and the small distance between two charges.
Electric Dipole Moment = charge ｘ Dipole length.
It is a vector quantity and is always directed in the direction from -q to +q along the line joining the two charges. It is also known as the direction of the dipole axis.
Unit: Cm (Coulomb Meter).
Dimensional Formula: [p] = [q][2a]
[p] = [AT][L] = [LTA]
Note that net charge on an electric dipole is always zero(0).
Electric Field due to a Dipole
At Axial Position
Consider Electric Dipole AB having +q and -q at a distance 2a.
O : center of dipole
P : point on axial position at distance 'r' from 'O' where Electric Field is required.
Dipole is kept in dielectric medium having constant : K
AB=2a
OA=OB=a
OP=r
AP=(r+a)
BP=(r-a)
Electric field at P due to charge +q :
E₁=k.q/(r-a)² ---eq(1)
It is directed along BP or along AB, same as the direction of p (dipole moment).
Electric Field at point P due to charge -q :
E₂=k.q/(r+a)²
directed along PA or opposite to AB, along -p.
Since, E₁ and E₂ are in opposite directions.
Net electric field at P :
vector(E) = vector(E1) + vector(E2)
Magnitude of electric field :
E=E₁-E₂ as E₁>E₂
Therefore,
E=(q/4Ï€∈₀K){[1/(r-a)²]-[1/(r+a)²]}
E=(q/4Ï€∈₀K){[(r+a)²-(r-a)²]/(r+a)²(r-a)²}
E=(q/4Ï€∈₀K){(r+a+r-a)(r+a-r+a)/[(r+a)(r-a)]²}
E=(q/4Ï€∈₀K)[2r.2a/(r²-a²)²]
or
E=(1/4Ï€∈₀K)[2(q.2a)r/(r²-a²)²]
Hence,
E = (1/4Ï€∈₀K)[2pr/(r²-a²)²] ...in the direction of dipole moment.
If r>>a
E=(1/4Ï€∈₀K)[2pr/(r²)²]
E=(1/4Ï€∈₀K)(2p/r³)
For air or vacuum K=1
Therefore, E=(1/4Ï€∈₀)(2p/r³)
⇒ E(axial) ∝ 1/r³
At Equatorial Position or Equatorial Plane
A plane drawn normal to dipole axis AB and passing through mid point 'O' of dipole length. Any point on the equatorial plane is said to be in equatorial position.
Consider Electric Dipole AB consisting of two charges -q and +q, separated by a small distance AB=2a. P is a point at distance 'r' from midpoint 'O' of dipole length AB and at equatorial position in the surrounding medium of dielectric constant K.
AB=2a
OA=OB=a
OP=r
AP=BP=√(r²+a²)
and let ∠PAB=∠PBA=0⁰ (zero degree).
Electric field at P due to charge +q:
E₁=(1/4Ï€∈₀K)[q/(√(r²+a²))²] along BP
or E₁=(1/4Ï€∈₀K)[q/(r²+a²)] along BP
Similarly, electric field at P due to charge -q:
E₂=(1/4Ï€∈₀K)[q/(√(r²+a²))²] along PA
or E₂=(1/4Ï€∈₀K)[q/(r²+a²)] along PA
Method 1
Now E₁=E₂ and both are at angle 0 with the direction parallel to dipole axis.
Resolving E₁ and E₂ into components along dipole axis and normal to dipole axis.
The components E₁.sinθ and E₂.sinθ i.e. normal to dipole axis are equal in magnitude.
E₁.sinθ = E₂.sinθ
and are opposite in direction, so cancel each other, while the components along the dipole axis are also equal in magnitude and are in the same direction so these add up to give resultant intensity of electric field at P.
E(net)=E₁.cosθ = E₂.cosθ
E(net)=2.(1/4Ï€∈₀K)[q/(r²+a²)]cosθ
Since, cosθ=OA/AP = a/√(r²+a²)
Therefore, E(net)=(1/4Ï€∈₀K)[q.2a/√(r²+a²)³]
or E(net)=(1/4Ï€∈₀K)[p/√(r²+a²)³]
For air or vacuum K=1
if r>>a
E=(1/4Ï€∈₀)(p/r³)
⇒ E(equatorial) ∝ 1/r³
Also, E(axial)/E(equatorial)=2
or in vector form, E(axial)=-2.E(equatorial)
Method 2
E = E₁ + E₂
E = √[(E₁)²+(E₂)²+2.E₁E₂.cos2θ]
Since, E₁=E₂=(1/4Ï€∈₀K)[q/(r²+a²)]=m (say)
and [cos2θ=2cos²Î¸ - 1]
Therefore, [1+cos2θ=2cos²Î¸]
E= √(m²+m²+2.m.m.cos2θ)
E= √[2m²(1+cos2θ)]
E= m√(4cos²Î¸)
E= 2m.cosθ
E= 2.(1/4Ï€∈₀K)[q/(r²+a²)]cosθ
Further calculation is the same as in method 1.
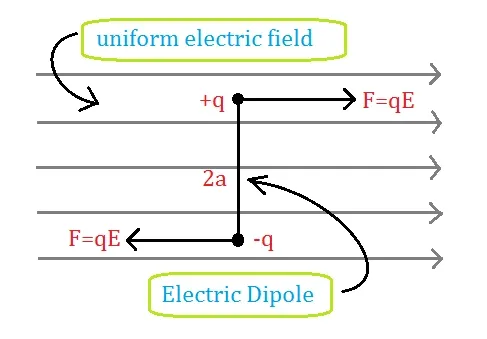
Electric Dipole In Uniform Electric Field
When an electric dipole is kept in a uniform electric field, a small couple applies a torque on the dipole which tends to align the dipole along the direction of uniform electric field.
Consider an electric dipole AB consisting of charges +q and -q at small distance 2a, and is kept in a uniform electric field of intensity E.
Dipole moment p makes angle 0 with direction of E (electric field).
+q charge experiences force due to the electric field (F=qE) along the direction of E.
-q charge experiences the same magnitude of force i.e. qE but in the opposite direction of the vector(E).
Two forces on a dipole are equal in magnitude and opposite in direction and have "parallel lines of action."
Net translation on dipole =
F+(-F) = qE-qE = 0
Hence no transnational motion of dipole in uniform electric field but such types of forces form a couple which tends to rotate the dipole.
Torque acting on dipole = moment of dipole
Torque = F.couple arm
Torque = F.Bc
Torque = qE.2asinθ
Torque = (q.2a).Esinθ
Torque = vector(p). vector(E)
When Dipole is Parallel to Field
p is in the same direction of E.
θ = 0⁰
Torque = p.E.sin(0⁰)
Torque = 0
"It is a stable equilibrium."
When Dipole is Anti-Parallel to Field
p is in the opposite direction of E.
0 = 180⁰
Torque = p.E.sin(180⁰)
Torque = 0
"It is an unstable equilibrium."
When Dipole is Perpendicular to Field
p is perpendicular to E, angle is 90⁰
Torque = p.E.sin(90⁰)
Torque = p.E.1
Torque = p.E (maximum Torque)
Angular Speed of Dipole Charges in Uniform Electric Field
We know that in circular motion, Linear Speed = Radius x Angular Speed
Therefore,
Angular Speed = (Linear Speed)/Radius
and here, Radius = Dipole Length/2 = 2a/2 = a
Linear Speed = Distance/Time
Linear Speed = aθ/t as distance = arc = θ.radius
Angular Speed = (aθ/t)/a
Angular Speed = θ/t
For 'n' circular rotations in time 't',
Angular Speed = 2nπ/t
0 Comments
Write your queries or share your ideas... just speak up, don't hesitate... ;)